L2 Softmax(2016,ECCV)
개요
Facerecognition 성능향상 방법중 Loss function 이용, 그 중에 classification loss 에 대한 내용이다.
이름에서 보다시피 원래 Classifciation에 사용되는 Softmax에 discriminative를 위해 무언가 추가한 형태같다.
설명
Face Recognition 에서 사용되는 Softmax에는 장단점이 있다.
장점
1. 여러 class를 손쉽게 구별
2. 이전에 살펴본 Contrastive loss나 Triplet Loss와 다르게 batch selection에 대한 제한이 없다.
-> 위 두개 Loss는 일일이, 또는 batch 내에서 sampling을 해줘야 했고, 이는 성능에 영향을 주었다.
3. 구현이 쉽다.
단점
1. Class가 많으면 memory가 부족하다.
2. training 과정에서 잘나온 이미지(high quality, 구별이 쉬운)에는 잘 적용되나, 어려운 이미지는 무시하게 된다.
해결방법
첫번째 단점은 dataset을 sample 해서 사용하게 되면 해결할 수 있고, 두번째를 해결하기 위해 L2 Softmax가 제안된다.
-> 2번에대한 negative effect에 대해 bound constraint을 주면, 즉 어려운 sample에 대해 좀더 attention을 주면 해결되지 않을까? -> model에 L2 normalization layer를 넣어 layer를 scailing 하자.
L2-Softmax Loss

위식을 보면 기본 softmax에 feature의 L2-norm을 alpha로 제한하는 'subject to' 부분 (constraint)만 생성됐다.
저자는 center loss같이 추가적인 loss를 넣기 싫어 single sequential network를 제안해 softmax에서 간단히 바꿀 수 있도록 했다.
L2norm의 효능
모든것은 'bad(hard)' sample에 집중하기 위함이다. 그러려면 good 이던 bad feature던 같은 hypershpere위에 올라가 비슷한 attention을 받으면 될것이다 라는 생각. (최근 트랜드인 논문들(SV-Softmax, Curricular Face)이랑 비슷하면서 완전히 다른 결론 도출함)



Norm Face( 2017,ACM MM)
개요
Facerecognition 성능향상 방법중 Loss function 이용, 그 중에 classification loss 에 대한 내용이다.
Deep Face(cvpr,2014)에서 Normalization은 testing phase에서만 사용, training에서 사용 x but normalization이 성능에 critical한것을 보고 training 과정에서도 normalization을 사용하자는 내용.
설명



Normalization 사용해야 하는 이유, Noramlize layer 설명
Euclidean distance의 단점예시 : 왼쪽사진에서 Euclidean distance를 사용하게되면 f1,f2는 가깝지만, f2,f3는 멀게된다. 하지만 실제 분류해야되는 Task에서는 f2,f3가 같은 class에 속한다.
softmax를 하게되면 위 figure2와 같이 'radia' feature distribution을 띄게된다. 왜냐하면 말그대로 soft version of max operator 이기때문에 manitude를 scaling 하는것은 class 선정에 영향을 미치지 않는다.
soft max 식은 다음과 같고 그에따른 class 분류식은 다음과 같다.


이때 bias가 없다 가정하면 다음 전제가 참이된다. bias가 있게되면 figure3 처럼 radial로만 분리가 불가하다


즉 soft max에서 확률값을 구하고 가장 높은 클래스를 뽑게되는데, 이때 feature의 크기에 따라 확률값이 달라지게된다. 따라서 softmax로 학습하게 되면 잘 구분되는 feature들은 큰 magnitude를 갖게 되는데 사실상 figure 2 에서 보듯이 어차피 'radial' 로 클래스를 분리하므로 이런 성질이 필요 없게된다. 원작자는 이런 현상을 없애기 위해 feature normalization을 제안한다.

위 사진에서는 feature의 embedding 이후 layer인 softmax에서 학습과정을 담고 있는데, feature를 normalizing 했으므로 hyper sphere(현재는 figure로 나타내기 위해 3차원) 의 표면에 존재하고 확대해보면 검은색 점(weight)의 학습시 다른 모든 feature의 loss들의 gradient를 합산한곳으로 weight를 움직인다. 검은색점은 빨간색 class에 해당하는 weight이므로 loss의 gradient를 상징하는 vector들은 hypersphere의 tangential 한 vector로 나타난다. 특히, 빨간색 점들에는 가까이 가려는 vector들로, 초록색, 주황색은 멀어지려는 vector들로 나타나는데 이 모든 vector들을 합하여 움직인다.
원문의 식과 설명은 다음과 같다.

Softmax Loss 바꾸기
training 에서 normalization 할 경우 학습이 잘 안되는 현상 발생. 기존 inner product로 logit을 사용 할 때에는 f와 w의 크기에 따라 범위가 (-20,20) , (-80,80)등으로 넓을 수 있으나 normalization 이후에는 logit의 범위가 [-1,1]로 줄어들어

아무리 잘 분리 되더라도 위식의 확률값이 1에 가까워지기 힘들게된다. 실제로 최대값은 W*f 값이 1일때 즉

=0.45가 최대값이 된다. 즉, 아래 전제와 같이 softmax 에 의한 loss의 lower bound가 생기게 되고 최대 학습 성능이 낮아진다.

위 문제를 해결하기 위해 본 논문에선 W*f를 s를 곱하여 scailing 해서 range를 늘려주었다. 바뀐 식은 아래와 같다.

Metric Learning 바꾸기
metric learning은 딱히 normalization을 했다고 학습에서 어려움이 생기진 않는다. 다만 n이 sample 개수라고 할때 classification의 학습 combination 경우의 수 O(n)과 다르게 O(n^2), triplet loss같은경우 pair를 뽑는데 O(n^3)의
complexity를 갖게 된다. 따라서 모든 sample에 대해 pair를 뽑기는 어렵고, 보통 hard mining 알고리즘을 통해 학습에 도움이 되는 sample들을 뽑는다.(최근트랜드). 하지만 본 논문에선 hard mining이 tricky, timeconsuming 하므로 O(n)을 유지하도록 metric learning을 수정하여 classifcation task를 수행하도록 했다.
아래 두식은 Metric learning의 대표적인 contrastive loss와 triplet loss의 식
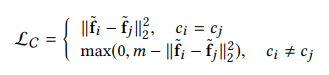
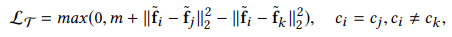
normalizing 한 softmax 식은아래와 같다.

because

식을보면 기존 softmax식에서 weight와 feature 사이의 L2 loss를 사용하는것처럼 보이므로, 기존 contrastive loss, triplet loss와 비슷하게 만들 수 있다.
(원문에서는 비교를 위해 classification version of the contrastive loss/triplet loss
-> C-contrastive loss, C-triplet loss 라 표현한다.)
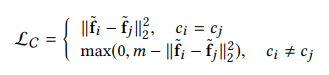

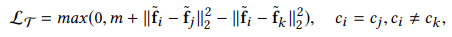
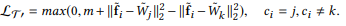
여기서 weight은 기존 Classification Task에서 Softmax가 사용되는 위치의 weight로 feature map(dimension = d ) 과 class 간의 맵핑을 하는 (d,n) 크기의 matrix를 말한다.

이렇게되면 기존 Softmax에서 사용되는 weight과 shape이 같으나 사용되는 의미에서는 softmax와 조금 다르게된다.
즉, Weight의 i-th columm은 i-th class를 대표하게 되는 vector를 의미하게 되므로, 식을 해석해보면
원래 contrastive loss, triplet loss에서 feature map끼리 비교하던것(left : (fi-fj)^2)을 feature mpa과 각 class를 대표하는 vector와 비교해서 가깝게, 또는 멀게 위치하도록 학습하게 된다((fi-Wj)^2).
1. 이때 학습하는 주체가 Softmax 자체일경우 Weight을 학습하면서 업데이트하므로 Weight vector의 위치를 feature map(위 그림에서 hyper sphere의 표면에 있는 점들)을 보고 바꾸게 되는것이고.
2. 학습하는 주체가 backbone network 일경우 feature map을 hyper sphere 상에서 어디에 위치 시킬지를 학습하게 된다.
현재 ArcFace나 CosFace처럼 margin 기반의 face recogntion 논문에서는 위 1번을 head/metric 이라고 부르고 있으며 2번을 backbone/network 라고 부르고 있다.
모델 수정에 대한 직관
Wj는 j-th class에 속한 feature들의 요약본(원문에서는 summarizer/ guide agent) 역활을 하므로 만약 margin에 의해 잘 분리되었으면 Wj는 각 class의 feature들의 means와 대략 비슷할 것이다. 하지만 더 복잡한 task 에서 초기에는 class가 다른 feautre들이 over lap 될 가능성이 있다.
이렇게되면 Wj들은 서로의 boundaries로부터 멀리 떨어질것이고, feature들도 Wj를 따라 서로 다른 클래스끼리 떨어도록 학습할 것이다.
또한 어려운 example(margin에 있는 feature)들 같운경우에는 gradient가 더 클것이므로 학습시 업데이트 되는 양이 커서 더 많이 움직일 것이다.
하지만 기존 metric learning에서 사용하던 margin을 똑같이 사용하게되면 margninal feature(어려운 sample)들은 optimize 되지 않으므로 더 큰 margin을 적용 시켜야한다. 간단히 말하자면 feature간의 차이보다 feature와 weight간의 차이가 더 클것이므로 margin을 늘려줘야 한다는얘기. 원문 전제는 다음과 같다.

실제로 실험적으로 feature, weight 차이로 구하는 distortion bound가 0.5~0.6에 위치하게 되는데, 원작자는 Contrastive 는 1, triplet loss는 0.8을 추천한다.
+ normailization을 하면서 scale의 크기가 고정되므로 모델에 맞는 적합한 margin 찾는것이 쉬워졌다.
Training
Proposed loss function은 feature layer 바로 뒤에 적용 되었다. Norm face의 이름답게 feature와 weight matrix의 column들은 L2-norm=1이 되도록 normalize 하고 w의 각 colum(agent)와 featrue를 inner product 하던지 Euclidean Distance 를 구해 Loss 를 구한후 Optimization 시킨다. (위쪽에서 언급한 C-contrastive loss or C-triplet loss)
결론
기존에 test 에만 적용되던 L2 Normalization을 training에도 적용시킴. normalization이 필요한 이유를 수치적으로, geolmetric관점 둘다 직관적으로 설명하였으며, 두가지 Loss function을 제안.
하나는 Softmax loss에서 normalization 할경우 학습에 제한이 생기는것을 막기위해 추가한 scale term, s.
다른 하나는 metric learning 기반으로 agent를 guide 삼아 softmax를 구현한 C-triplet, C-contrastive loss이다. 두번째는 특히 기존 metric learning에서 discriminative한 성능을 가지는 hard sample mining의 장점은 살리되 time-consuming 한 단점을 획기적으로 줄이는 방법이다. 이후에 이 논문의 두번째 방법을 바탕으로 변형을 거친 논문들(margin based Loss)이 많이 나오게 되고 SOTA를 계속 갱신하게 되는데, 이는 다음글에서 서술 하겠다.
출처
:[1] R. Ranjan , "L2-constrained Softmax Loss for Discriminative Face Verification", 2017
[2] L2 softmax 설명 블로그
[3] F. Wang, Norm Face: Hypersphere Embedding for Face verification., ACM MM, 2017.
L2-constrained Softmax Loss for Discriminative Face Verification
In recent years, the performance of face verification systems has significantly improved using deep convolutional neural networks (DCNNs). A typical pipeline for face verification includes training a deep network for subject classification with softmax los
arxiv.org
L2-constrained Softmax Loss for Discriminative Face Verification
Introduction
medium.com
NormFace: L2 Hypersphere Embedding for Face Verification
Thanks to the recent developments of Convolutional Neural Networks, the performance of face verification methods has increased rapidly. In a typical face verification method, feature normalization is a critical step for boosting performance. This motivates
arxiv.org
slideplayer.com/slide/14707829/
NormFace: - ppt download
Motivation DeepFace: Closing the Gap to Human-Level Performance in Face Verification, Taigman et. al. , CVPR 2014 𝐿 2 normalization is applied only on the testing phase.
slideplayer.com
'인공지능 > Face Recognition' 카테고리의 다른 글
| [Paper Review] MV-Softmax (SV-Softmax, SV-X-Softmax) 정리 (0) | 2021.02.09 |
|---|---|
| Face Recognition 트렌드 정리 (0) | 2021.01.29 |
| [Paper Review] Center loss 정리 (4) | 2021.01.27 |
| Triplet Loss, Triplet Mining 정리 (5) | 2021.01.27 |
| Open set/ Closed set 에 따른 Identification/Verification + Contrastive Loss 정리 (2) | 2021.01.26 |