E개요
IJB-C Identification code 를 돌려 결과를 확인하는 중 probe, gallery에 대한 개념과 성능 분석에 어려움이 있어 빨리 읽은 논문. 2017 CVPR Biometric 부분.

항목별 요약
알게된 점을 항목별로 요약하자면 다음과 같고, 용어나 개념에 대한 자세한 설명은 다음 꼭지에서 다룸.
(Gallery)
- Gallery는 training data중 인식하고자 하는 인물의 사진들(혹은 임베딩된 feature들)을 담은 집합이다.
- Enrollment는 Gallery를 설정하고 학습하는 과정
(위 사진에서 Training 중 초록색이 Gallery 부분)
(Probe)
- Probes는 Identification task를 수행하길 원하는 data
- querying은 probe로 identifcation 하는 과정.
(Open Set)
- IJB같은 경우 1:N Identifcation은 closed-set evaluation.
- Gallery에 없는 예외 데이터 처리를 위해선 Open set 에서 rejection/ignore 하는 방법이 필요함
- rejection 방법으로 본 논문에선 세가지 방법을 제시
1. verification Threshold
2. linear discriminant analysis(LDA)
3. extreme value machine(EVM)probability
- 결과적으로, 1은 closed set은 좋지만 open set에선 안좋았다
- 2는K( known unknown)에선 좋지만 U(unknown unknown)에선 안좋았다.
- 3은 K,U 둘다 에서 좋았다.
(성능 비교 포맷)
~보통 verification(선택지가 0/1)의 경우 roc curve를 그리는데 identifcation(선택지가 #class,N개)은 성능평가를 어떻게 해야하나 궁금. 본 논문에선 3가지 방법 활용.
1. Cumulative match Characteristics(CMC) curves
2. Receiver Operating Charcateristics(ROC) curves
3. Detection and Identification rate (DIR) curves
----> 일반적으로 쓰는 curve는 아닌것같고 Face Recognition handbook에서 나왔다고함.
상세, 추가 조사
1. LDA
: 데이터 분포를 학습해 class내 분산은 작게 하면서 class간data들의 평균점을 멀게하는 결정경계(직선)을 찾는 모델
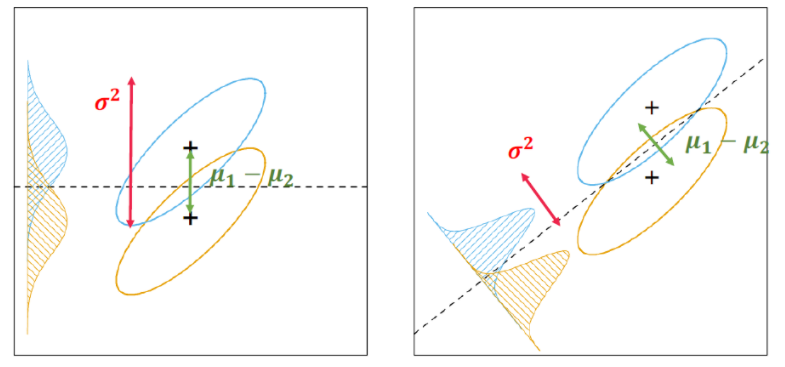
-출처 :
[머신러닝 스터디] LDA (Linear Discriminant Analysis)
데이터 분포를 학습해 결정경계를 만들어 데이터를 분류하는 모델(어느 모델이 더 분류가 잘 되었다고 판단할 수 있을까?)두 범주의 중심(평균!)이 서로 멀수록 좋다!두 범주의 분산이 작을수록
velog.io
2. EVM
Extreme value theory를 이용하여 point별로 distribution추출 후 해당 클래스의 속하는지 확률 구함.
-출처 :
https://www.researchgate.net/publication/278969514_The_Extreme_Value_Machine
(PDF) The Extreme Value Machine
PDF | This paper provides a novel characterization of the max-margin distribution in input space. The use of the statistical Extreme Value Theory (EVT)... | Find, read and cite all the research you need on ResearchGate
www.researchgate.net
3. CMC curve

CMC(Cumulative Match Characteristic) 곡선 시험이란,「Top N 순위 안에서 인식이 되는가?」를 판정하는 식별 시나리오에서 성능을 분석하는 가장 대표적인 시험방법이다. 이 CMC 곡선은 순위에 대한 함수로서, x축에 순위를 나타내고, y축에는 누적된 인식률을 나타내는 것에 의해, n번째 순위까지의 프로브에 대한 인식률을 확인할 수 있다.
-출처 :
https://patents.google.com/patent/KR20060068796A/ko
KR20060068796A - 얼굴인식 시스템의 성능시험 방법 및 시스템 - Google Patents
얼굴인식 시스템에서 트레이닝 대상이 되고, 성능 시험에서 갤러리가 되는 영상들의 집합인 대상(Target) 집합과 성능 시험에서 프로브가 되는 영상들의 집합인 질의(Query) 집합으로 이루어진 xml
patents.google.com
4. ROC curve
정리가 아주 잘되어 있어 출처로 대신함.
x축 : False Positive Rate
y축 : True Positive Rate
-출처 :
https://angeloyeo.github.io/2020/08/05/ROC.html
ROC curve - 공돌이의 수학정리노트
angeloyeo.github.io
5. DIR curve
Face Recognition 분야에서만 쓰이는 그래프로 보임.
이름에 Detection이 들어가 있지만 본 논문에서 detectionn은 된다고 가정하므로
y축: Identifcation rate
x축: False Alarm Rate(False Positive Rate)
즉 CMC의 x축을 rank가 아닌 FPR로 대체한 그래프
출처
https://ieeexplore.ieee.org/document/6365193?source=post_page---------------------------
Toward Open Set Recognition
To date, almost all experimental evaluations of machine learning-based recognition algorithms in computer vision have taken the form of “closed set” recognition, whereby all testing classes are known at training time. A more realistic scenario for visi
ieeexplore.ieee.org
'인공지능 > Face Recognition' 카테고리의 다른 글
| IJB-C 공개 데이터 사용법(How to use IJB-C Dataset) (13) | 2021.06.12 |
|---|---|
| [Paper Review] AdaCos 정리. (0) | 2021.05.13 |
| Arc Face Easy Margin에 대해 (0) | 2021.03.09 |
| [Paper Review] Curricular Face 정리 (0) | 2021.02.23 |
| [Paper Review] MV-Softmax (SV-Softmax, SV-X-Softmax) 정리 (0) | 2021.02.09 |